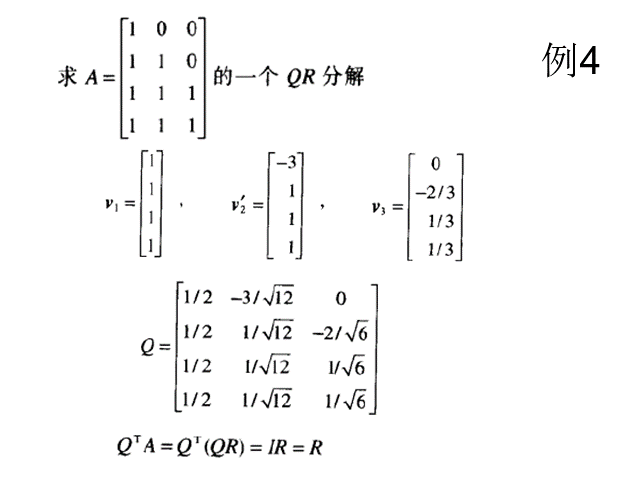第一章线性代数中的线性方程组

线性方程组

线性方程组由一个或多个线性方程组成。例：
$2x_1-x_2+1.5x_3=8$
$\ \ x_1-\ \ \ \ \ \ \ \ \ \ \ \ 4x_3=-7$

线性方程组的解是一组数$(s_1,s_2,···,s_n)$，用这组数分别替代$x_1,x_2,···,x_n$时所有方程的两边相等。

解集：方程组所有可能的解的集合称为线性方程组的解集。

若两个线性方程组有相同的解集，则称它们为等价的。

线性方程组的解有以下三种情况：

无解
有惟一解
有无穷多解

方程组有解，称为方程组相容（consistent）；无解称为不相容（inconsistent）。

方程组的矩阵形式

初等行变换：

（倍加变换）把某一行换成它本身与另一行的倍数的和。
（对称变换）把两行对换。
（倍乘变换）把某一行的所有元素乘以同一个非零数。

一次初等行变换是可逆向进行的。A矩阵经过一次初等行变换到B矩阵，则B矩阵经过一次初等行变换到A矩阵。可以验证多次初等行变换也是可逆向进行的。

行等价（row equivalent）：两个矩阵称为行等价，如果存在一系列初等行变换使一个矩阵变到另一个矩阵。

矩阵的行等价是一种等价关系。

若两个线性方程组的增广矩阵是行等价的，则它们具有相同的解集。

方程组的基本问题：

方程组相容吗？
方程组的解的个数唯一吗？
行化简与阶梯型矩阵

非零行的先导元素：左面第一个非零元素

矩阵如果满足下面三个条件，则称为（行）阶梯型（(row)echelon form）矩阵：

每一非零行在每一零行之上；
某一行的先导元素所在的列位于前一行先导元素的右面；
某一先导元素所在列下方元素都是零。

若一个阶梯型矩阵还满足以下性质，称它为简化阶梯型（(row)reduced echelon form）矩阵：

每一非零行的先导元素是1；
每一先导元素1是该元素所在列的惟一非零元素。

定理1（简化阶梯型矩阵的惟一性）：
每个矩阵行等价于惟一的简化阶梯型矩阵。

阶梯型的先导元素的位置是固定的，称为主元位置（pivot position）。

主元位置的非零元素称为主元（pivot）。

主元位置所在的列称为主元列（pivot column）。

一个矩阵的行化简得到的阶梯型不一定相同，但主元位置和主元列一定相同。

基本变量：对应于主元列的变量。

自由变量：非主元列的变量。

方程组的通解：所有解的显式表示。

定理2（存在与惟一性定理）：
线性方程组相容的充要条件是增广矩阵的左右列不是主元列，就是说，增广矩阵的阶梯型没有形如
$[0\ ··· 0 \ b]\ b\ne 0$
的行。若线性方程组相容，它的解集可能有两种情形：（i）当没有自由变量时，有惟一解；（ii）当至少有一个自由变量时，有无穷多解。

向量方程

仅含一列的矩阵称为列向量，或简称向量。

$w=[\begin{matrix}
w_1\
w_2\
\end{matrix}]$

$w_1$和$w_2$为任意实数。所有两个元素的向量的集记为$R^2$，$R$表示向量中的元素是实数，而指数2表示每个向量包含两个元素。

$R_2中两个向量相等，当且仅当对应元素相等。因此，[\begin{matrix}4\\7\end{matrix}]和[\begin{matrix}7\\4\end{matrix}]是不相等的。$ $[\begin{matrix}1\\-2\end{matrix}]+[\begin{matrix}2\\5\end{matrix}]=[\begin{matrix}1+2\\-2+5\end{matrix}]=[\begin{matrix}3\\3\end{matrix}]$ $若\mathbb{u}=[\begin{matrix} 3\\1 \end{matrix}],c=5,则c\mathbb{u}=5[\begin{matrix}3\\-1\end{matrix}]=[\begin{matrix}15\\-5\end{matrix}]$

数c称为标量

$R^n$中向量的代数性质：
$对R^n中一切向量\mathbb{u,v,w}以及标量c和d$，

$\mathbb{u}+\mathbb{v}=\mathbb{v}+\mathbb{u}$
$(\mathbb{u}+\mathbb{v})+\mathbb{w}=\mathbb{u}+(\mathbb{v}+\mathbb{w})$
$\mathbb{u}+\mathbb{0}=\mathbb{0}+\mathbb{u}=\mathbb{u}$
$\mathbb{u}+(\mathbb{-u})=\mathbb{-u}+\mathbb{u}=\mathbb{0}$
$c(\mathbb{u}+\mathbb{v})=c\mathbb{u}+c\mathbb{v}$
$(c+d)\mathbb{u}=c\mathbb{u}+d\mathbb{u}$
$c(d\mathbb{u})=(cd)(\mathbb{u})$
$1\mathbb{u}=\mathbb{u}$

$给定R^n中向量v_1,v_2,···,v_p和标量c_1,c_2,···,c_p$，向量
$\mathbb{y}=c_1\mathbb{v_1}+···+c_p\mathbb{v_p}$
称为向量$v_1,v_2,···,v_p以c_1,c_2,···,c_p为权的线性组合$。

定义：
若 $\mathbb{v_1,v_2,···,v_p}$ 是 $R^n$ 中的向量，则 $\mathbb{v_1,v_2,···,v_p}$ 的所有线性组合所成的集合用记号 $Span\{\mathbb{v_1,v_2,···,v_p}\}$ 表示，称为由 $\mathbb{v_1,v_2,···,v_p}$ 所生成（或张成）的 $R^n$ 的子集。也就是说， $Span\{\mathbb{v_1,v_2,···,v_p}\}$ 是所有形如

$c_1\mathbb{v_1}+c_1\mathbb{v_2} +···+c_p\mathbb{v_p}$

的向量的集合，其中 $c_1,c_2,···,c_p$ 为向量。

矩阵方程$A\mathbb{x}=\mathbb{b}$

定义：

$\begin{aligned}A\mathbb{x} &=\left[ \begin{matrix}a_1\ a_2\ ···\ a_n\end {matrix} \right] \left[ \begin{matrix}x_1\\ x_2\\ ···\\ x_n\end{matrix} \right] \\ &=x_1\mathbb{a_1}+x_2\mathbb{a_2}+···+x_n\mathbb{a_n} \end{aligned}$

$A\mathbb{x}=\mathbb{b}有解\iff \mathbb{b}是A的列向量的线性组合$

定理4：
$1. 对R^m中每个\mathbb{b}，方程A\mathbb{x}=\mathbb{b}有解。$
$2. R^m中的每个\mathbb{b}都是A的列的一个线性组合。$
$3. A的各列生成R^m。$
$4. A在每一行都有一个主元位置。$

定理5：

$A(\mathbb{u}+\mathbb{v})=A\mathbb{u}+A\mathbb{v}$
$A(c\mathbb{u}=c(A\mathbb{u}))$

线性方程组的解集

齐次线性方程组（Homogenous Linear System）：$A\mathbb{x}=\mathbb{0}$

平凡解（trivial solution）：$\mathbb{x}=\mathbb{0}$

非平凡解（nontrivial solution）：非0解

有非平凡解$\iff$有自由变量

齐次方程组的解的结构：几个向量张成的空间，$span{v_1,v_2,···,v_p}$。

定理6：$如果A\mathbb{x}=\mathbb{b}有解，设\mathbb{p}是一个特解，通解结构：\mathbb{p}+(A\mathbb{x}=0的通解)$

如果$A\mathbb{x}=0$只有0解，则$A\mathbb{x}=\mathbb{b}$只有一个特解。

将非齐次线性方程组右端的常数换为零，得到的齐次线性方程组称为该非齐次线性方程组的导出组。

线性无关

对于$R^n$的一系列向量${v_1,v_2,···,v_p}$，若满足
$x_1v_1+x_2v_2+···+x_pv_p=0$
有惟一的平凡解，则这组向量是线性无关的。

如果有0向量，则线性相关

线性变换介绍

$Ax=b$

$x_1a_1+x_2a_2+···+x_na_n=b$

Ax写法强调了A作用到x的变化

线性变换：一个变换T是线性的需要满足：
$对于定义域内所有的向量u和v，有T(u+v)=T(u)+T(v)$
$对于任意向量u和任意参数c，有T(cu)=cT(u)$

矩阵变换是线性变换

线性变换的性质：

$T(0)=0$
$T(cu+dv)=cT(u)+dT(v)$

线性变换的矩阵

线性变换的标准矩阵是唯一的。

映上： $R^m中的每个b向量是至少一个R^n中x向量的像，则变换T:R^n→R^m是映上R^m的。$

一对一：$R^m中的每个b向量是至多一个R^n中x向量的像，则变换T:R^n→R^m是一对一的。$

定理11：$T:R^n→R^m是线性变换。那么，T是单射\iff T(x)=0只有平凡解$

定理12：$T:R^n→R^m是线性变换，A是T的标准矩阵，那么$
$T是满射\iff A的列向量张成R^m$
$T是单射\iff A的列向量线性无关$

第二章矩阵代数

矩阵运算

定理1：

A+B=B+A
(A+B)+C=A+(B+C)
A+0=A
r(A+B)=rA+rB
(r+s)A=rA+sA
r(sA)=(rs)A

一般情况下，$AB\ne BA$

若$AB=AC$，一般情况下，B=C不一定成立。

定理3：

$(A^T)^T=A$
$(A+B)^T=A^T+B^T$
$任意数r，(rA)^T=rA^T$
$(AB)^T=B^TA^T$

矩阵的逆

对于n×n矩阵A，若有一个n×n矩阵C满足$CA=AC=I_n$，则A是可逆的。C是A的逆矩阵。

逆矩阵有唯一性。

不可逆的矩阵叫奇异矩阵，可逆矩阵叫非奇异矩阵。

定理5：$若A是n×n矩阵，则R^n中的每个向量b，Ax=b有唯一解x=A^{-1}b$

定理6：

$(A^{-1})^{-1}=A$
$(AB)^{-1}=B^{-1}A^{-1}$
$(A^T)^{-1}=(A^{-1})^T$

对单位矩阵进行一次初等行变换，得到初等矩阵。

初等矩阵E左乘一个矩阵A，EA $\iff$ 对A进行对应的初等行变换。

初等矩阵E是可逆的。

定理7：$n\times n矩阵可逆 \iff A行等价于I$

可逆矩阵的特征

定理8（可逆矩阵定理）：

A是可逆矩阵。
$A等价于n \times n单位矩阵。$
A有n个主元位置。
方程Ax=0仅有平凡解。
A的各列线性无关。
线性变换$x|→Ax$是一对一的。
$对R^n中的任意b，Ax=b至少有一个解。$
$A的各列生成R^n$
$线性变换x|→Ax把R^n映上到R^n上。$
$存在n \times n的矩阵C使CA=I$
$存在n \times n的矩阵使AD=I$
$A^T是可逆矩阵$

分块矩阵

定理10：若A是m×n矩阵，B是n×p
矩阵，则
$AB=[col_1(A)\ col_2(A)\ ··· col_n(A)] \left[ \begin{matrix} row_1(B)\
row_2(B)\
···\
row_n(B)
\end{matrix} \right]$

矩阵因式分解

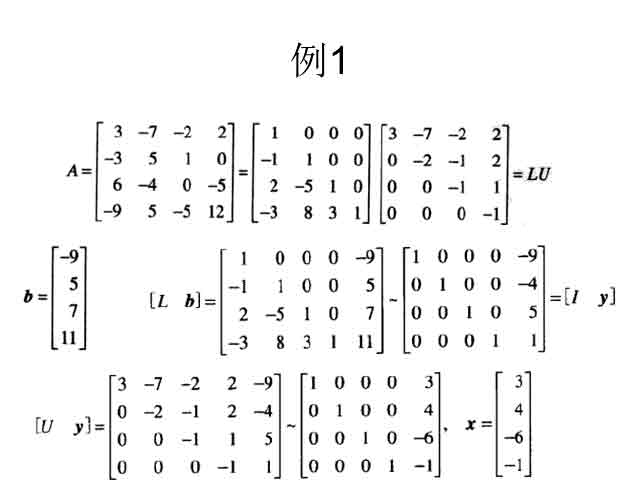
LU分解

第三章行列式

行列式介绍

矩阵A的行列式记为detA

去掉第i行第j列所在的行和列，得到的子矩阵$A{ij}$，叫A的子行列式（也叫余子式）。$C{ij}=(-1)^{i+j}detA_{ij}$是A的代数余子式。

定理1：$det A = a{i1}C{i1}+a{i2}C{i2}+···+a{in}C{in}$

定理2：三角矩阵的行列式等于主对角线上元素的乘积。

行列式的性质

定理3 设A是一个方阵，则：

矩阵A的一行的乘积加到另一行得到矩阵B，detA=detB.
矩阵A的两行交换得到矩阵B，则detB=-detA.
矩阵A的一行乘k得到矩阵B，则detB=k·detA.

定理4：$方阵A可逆\iff detA \ne 0$

定理5：$若A是一个n \times n矩阵，则detA^T=detA$

定理6：若A、B是一个n×n矩阵，则detAB=(detA)(detB)

克拉默法则、体积和线性变换

对于方程组Ax=b，记：$A_i(b)=[a_1 ··· b ··· a_n]$

定理7（Cramer法则）：A是可逆的n×n矩阵，Ax=b的惟一解是$x_i=\frac{detA_i(b)}{detA}$

定理8（逆矩阵公式）：设A是一个可逆的n×n矩阵则$A^{-1}=\frac{1}{detA}adjA$
其中 $adjA=\left[ \begin{matrix}C_{11} & C_{21} & ··· & C_{n1}\\ C_{12} & C_{22} & ··· & C_{n2}\\ ··· & ··· & ··· & ···\\ C_{1n} & C_{2n} & ··· & C_{nn}\end{matrix}\right]$

第四章向量空间

向量空间与子空间

向量空间V的子空间是V的一个子集H且满足：

V中的零向量在H中。
H内的任意的u、v两向量，u+v也在H内。
H内的任意向量u和任意数c，cu在H内。

只有0向量的空间是任何向量空间的子空间，称为0空间，写作{0}

$R^2不是R^3的子空间，因为R^2不是R^3的子集$

称 $\mathrm{Span} \{v_1,v_2,···,v_p\}为\{v_1,···,v_p\}$ 张成的子空间

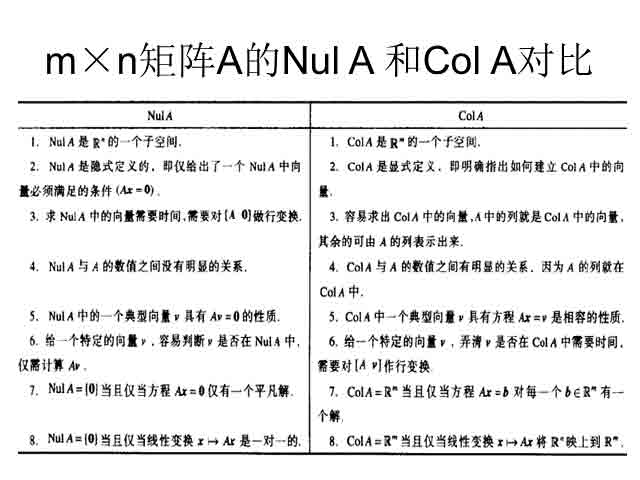
零空间、列空间和线性变换

满足Ax=0的所有x的集合为矩阵A的零空间

m×n矩阵A的列空间ColA是A列向量所有线性组合的集合。

定理3：m×n矩阵A的列空间是$R^m$的子空间

线性变换的核是V中满足T(u)=0的所有向量u的集合。

线性无关集和基

设H是向量空间V的一个子空间，V中的向量集$B={b_1,b_2,···,b_p}$称为H的一组基，如果：
(i)B是线性无关集
(ii)B生成H，即$H=Span{b_1,···,b_p}$

矩阵的行初等变换不改变列向量的相关性

定理6：矩阵A的主元列是colA的一组基。

坐标系

令$B={b_1,b_2,···,b_n}$是向量空间V的一组基，则对于V中的任一向量x，存在唯一一组标量$c_1,···,c_n$使得$x=c_1b_1+···+c_nb_n$

坐标映射是一一对应线性变换

向量空间的维数

如果向量空间V有一组基$B={b_1,···,b_n}$，那么V中任何多于n个的向量集合一定是线性相关的。

定理10：如果向量空间V有一组基有n个向量，那么它的每一组基都有n个向量。

NulA的维数是自由变量的个数，ColA的维数是主元列的个数。自由变量的个数+主元列的个数=A的列数

秩

A的行向量生成的空间称为行空间，记为rowA。

$colA^T$和rowA是相同的空间

行化简改变行向量之间的线性相关性，但不改变行空间的维数，不改变行空间；行化简不改变列向量之间的线性相关性，不改变列空间的维数，但改变列空间。

定理13：两个矩阵A、B行等价，则行空间相同，如果B矩阵式阶梯型，则其非零行向量就是行空间的基。

行空间和列空间的维数相等，称为矩阵A的秩。

m×n矩阵A：rankA+dimNulA=n

可逆矩阵定理（续2.3节）

A的列构成$R^n$的一个基
$ColA=R^n$
dimColA=n
16.rankA=n
NulA={0}
dim NulA=0

基的变换

$设B={b_1,···,b_n}和C={c_1,···,c_n}是向量空间V的基，则存在一个n \times n的矩阵\underset{C←B}{P}使[x]_C=\underset{C←B}{P}[x]_B$
$\underset{C←B}{P}$称为B到C的坐标变换矩阵。

定理15：坐标变换矩阵的列向量使线性无关的
于是成立 $\big(\underset{C←B}{P}\big)^{-1}[x]_C=[x]_B$ $\big(\underset{C←B}{P}\big)^{-1}=\underset{B←C}{P}$

第五章特征值与特征向量

特征向量与特征值

对于n×n的矩阵A，如果存在x（≠0）满足：Ax=λx（λ为标量），则称x为特征向量，λ称为该特征向量的特征值。

特征向量一定≠0，特征值可以是0

对于一个特征值λ，方程组的零空间称为λ的特征空间。特征空间中的向量都是λ的特征向量（0除外）

定理1：三角形矩阵的特征值是对角线的元素

特征方程

det(A-λI)=0称为特征方程

det(A-λI)称为特征多项式

n×n矩阵A和B，如果存在矩阵P，使得$A=PBP^{-1}$，则称A相似于B。

A相似于B，则B相似于A。称为A和B相似。

定理4：如果n×n矩阵A和B相似，则有相同的特征值（重数也相同）。

相似不改变特征值，行等价改变特征值

相似不改变行列式的值，行等价改变行列式的值。

相似和行等价都是等价关系，都不改变维数、秩。

对角化

$A=PDP^{-1}$，其中D是对角线矩阵

如果存在矩阵P和D，使得$A=PDP^{-1}$，则称A可对角化

定理5：n×n矩阵A可对角化$\iff$ A有n个线性无关的特征向量。

可对角化条件：存在矩阵P和D，使得$A=PDP{-1}$，此时P的各列都是A的特征向量，D的对角线元素是A的特征值。

定理6：n×n矩阵如果有n不同的特征值，则可对角化。

第六章正交性和最小二乘法

内积、长度与正交性

$u^Tv$称作u和v的内积，记为u·v，也成为点积。

$u·v=v·u$

定理1：u，v，w是$R^n$中的向量，c是常数。则

$u · v = v · u$
$(u + v) · w = u · w + v · w$
$(cu)·v=c(u·v)=u·(cv)$
$u·u\ge 0 且u·u=0\iff u=0$

$R^n$中的两个向量u、v如果u·v=0则成为互相垂直（正交）。

0向量与所有向量正交。

正交集

$R^n中的几个向量{u_1,···,u_p}，如果任两个不同向量都正交，则称为正交向量集。$

格拉姆-施密特方法

最小二乘问题

$A^TAx=A^Tb$

定理14：$A^TA可逆\iff A的列向量线性无关$

第七章对称矩阵和二次型

对称矩阵的对角化

满足$A^T=A的矩阵A是对称矩阵$

对称矩阵一定是方阵

可正交对角化：$A=PDP^T=PDP^{-1}$ 一定是对称矩阵

定理2：一个n×n矩阵可正交对角化$\iff$ A是对角矩阵

二次型

二次型是二次函数$Q(x)=x^TAX$其中A是n×n对称矩阵，称为二次型的矩阵。

二次型可通过变量代换去掉交叉乘积项。

线性代数笔记

第一章 线性代数中的线性方程组